Anlamak istediğimiz sistemin daha önce hiç karşılaşılmadığı ve sadece birkaç dağınık gözlem mevcut olduğunda ne yapmalıyız?
Birçok alanda ortaya çıkan bir senaryo: vahşi doğada zor bir hayvanı izleyen bir biyolog, sadece birkaç kez kliniğe gelebilecek bir hastayı izleyen bir tıbbi araştırmacı ve uzak bir yerde hatalı bir sensöre sahip bir çevre bilimcisi. Tüm bu durumlarda, veriler seyrekyani, sadece eksik değil, aynı zamanda düzensiz ve öngörülemeyen yollarla eksik.
Bu durumlarda makine öğrenimi yardımcı olabilir. Ancak işte şu: Çoğu makine öğrenimi yöntemi, ilginizdeki sistemden çok sayıda eğitim verisi gerektirir. Bu olmadan, sistemin dinamik kurallarını “öğrenemezler”. Bu soruyu sorduk: Diğer sistemlerden öğrenen makine öğrenimi tabanlı bir yaklaşım tasarlayabilir miyiz, daha sonra tamamen yeni, görünmeyen bir sistemin dinamiklerini sadece seyrek ölçümlerden yeniden yapılandırmak için bu bilgiyi uygulayabilir miyiz?
Seyrek ve rastgele verilerin zorluğu
“Tam” verilere atıfta bulunurken, genellikle bir sinyalde yeterli bilgi yakalamak için altın standart olan Nyquist kriterini karşılayan düzenli aralıklarla toplanan veriler anlamına gelir. Seyrek, rastgele veriler standardı iki şekilde ihlal eder: (1) Veri noktaları zamanla, öngörülebilir bir model olmadan dağılmıştır ve (2) gözlemlenenden daha fazla nokta eksiktir.
Kaotik sistemlerde (küçük değişikliklere karşı zarif bir şekilde duyarlı olanlar), bu boşluklar yeniden yapılanmaya ölümcül olabilir. Parkur boyunca sadece altı puan görürseniz, bir rollercoaster'ın yolunu tahmin etmeye çalıştığınızı düşünün. Bazı uzatmalar için, noktaları bağlamanın sonsuz birçok yolu vardır.
Hayal kırıklığından melez bir çözüme
Hedef sistemin seyrek gözlemleri üzerinde bir makine öğrenme modelinin doğrudan eğitilmesinin işe yaramayacağını biliyorduk, çünkü bu gözlemler sahip olduğumuz tek şey olabilir. Böylece, olağan süreci çevirdik:
- Tamamen üzerinde bir model eğitin sentetik Düzinelerce iyi bilinen kaotik sistemlerden elde edilen veriler (ancak hedef değil).
- Bu eğitimli modeli yeni sistemden seyrek gözlemleri verin ve pürüzsüz ve sürekli yörüngeyi yeniden yapılandırmasına izin verin.
- Uzun vadeli dinamikleri tahmin etmek için yeniden yapılandırılmış zaman serilerini ikinci bir makine öğrenme modeline ayırın.
1. ve 2. adım için seçtik transformatöruzun menzilli bağımlılıkları yakalama ve değişen uzunluklardaki dizilere uyum sağlama yeteneği nedeniyle doğal dil işlemede yaygın olarak kullanılan bir mimari. Eğitim sırasında, her adımda sistem, dizi uzunluğu ve seyreklik seviyesi seçimini randomize ettik. Bu “üçlü rastgelelik”, transformatörün herhangi bir sistemi ezberlemesini engelledi ve çeşitli sistemlerin kaotik dinamiklerinin genel kurallarını öğrenmeye zorladı.
3. adım için kullandık rezervuar hesaplamaYeterli kaliteli veri gördüğünde kaotik sistemlerin uzun vadeli davranışlarını tahmin etme geçmişine sahiptir.
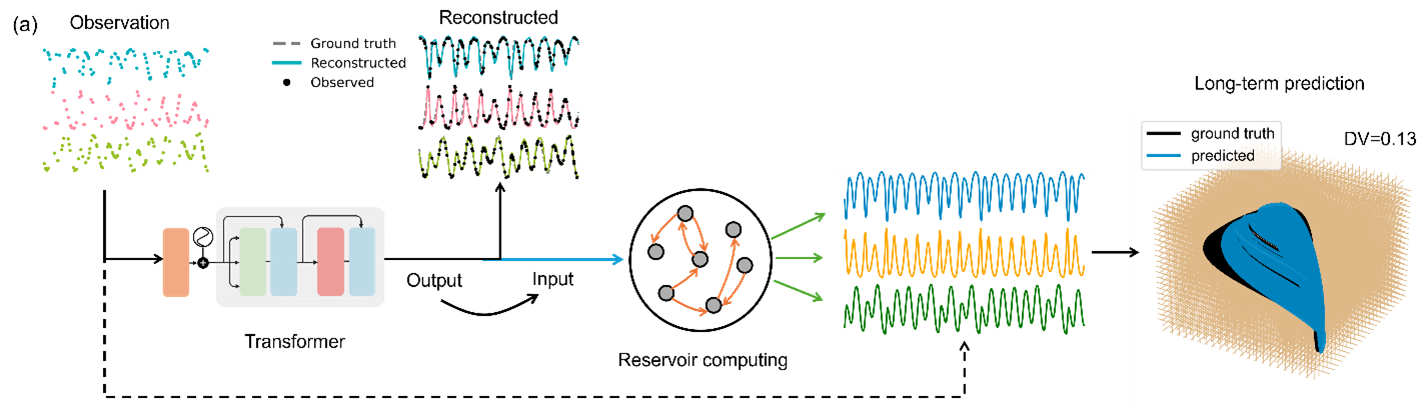
Dinamik rekonstrüksiyon için hibrit transformatör ve rezervuar bilgi işlem çerçevesi. Transformatör tarafından yeniden yapılandırılan zaman serisi, keyfi uzunluktaki hedef sistemin zaman serisini üreten ve temel gerçeği kabul eden yeniden yapılandırılmış bir çekiciye yol açan rezervuar bilgisayarını eğitmek için kullanılır.
Çerçeveyi test etmek için üç hedef sistem seçtik: kaotik üç tür gıda zinciri modeli, klasik Lorenz sistemi ve Lotka-Volterra sistemi.
Gıda zinciri sistemini örnek olarak alın. Hibrit makine öğrenme çerçevemizi, puanların sadece% 14'ünün verildiği, rastgele dağıldığı bir zaman serisini yeniden inşa etmek için eğittik. Bu noktalara bakan bir insan temel salınımları tahmin edemezdi. Yine de, transformatör boşlukları doldurdu, her türün popülasyonunun doğru yukarı ve aşağı ritimlerini yakaladı.
Neden sadece enterpolasyon yapmıyorsunuz?
Doğrusal veya spline enterpolasyonu, küçük bir veri eksik olduğunda iyi çalışır. Ancak yüksek sürede, bu yöntemler başarısız olur. Altta yatan dinamikleri anlamadan noktaları birbirine bağlarlar. Buna karşılık, makine öğrenme çerçevemiz, kaotik sistemlerin nasıl geliştiğini çıkarmak için sentetik eğitiminden öğrenir. Çerçevemiz sıkıştırılmış algılama ve diğer makine öğrenme modellerinden daha iyi performans gösterir.
Bu neden önemli?
Hibrit çerçeve, daha önce makine öğrenimine “sınırlar dışı” olan sistemleri incelemenin bir yolunu sunar: (1) hedef sistemden eğitim verisi gerekli değildir, (2) aşırı veri seyrekliği altında çalışır ve (3) görünmeyen sistemlere genelleme yapabilen.
Potansiyel uygulamalar ekoloji, iklim bilimi, tıp ve mühendislik, yani her yerde kritik kararlar eksik, düzensiz ölçümleri anlamlandırmaya bağlıdır. Örneğin, giyilebilir sağlık monitörleri, piller öldüğünde veya cihazlar çıkarıldığında genellikle büyük veri parçalarını kaçırır. Yaklaşımımız, sağlık olayları için erken uyarılar sağlayarak bu parçalardan sürekli hayati işaretli zaman serilerini yeniden inşa edebilir.
İleriye Bakış
Bu çalışmanın en heyecan verici yönlerinden biri, dinamik sistemler için bir temel modelinde geliştirilebileceğidir. Hesaplamalı deneylerimizde, yeniden yapılandırma hatası, eğitim sistemlerinin çeşitliliğini artırdıkça bir güç yasası eğilimi izledi, bu da yeterli çeşitlilikle, modelin sınıfındaki neredeyse her şeye genelleştirebileceğini düşündürdü.
Önümüzdeki yol, otonom olmayan sistemlerin üstesinden gelmeyi, yeniden yapılanma paradigmasının teorik sınırlarını anladığımızı ve gerçek dünya veri senaryolarında test edilmeyi içerir.
Bir hayal kırıklığı olarak başlayan şey (çalışmak istediğimiz sistemde antrenman yapamadığımız), bu zorluk üzerinde başarılı olan bir yönteme dönüştü. Bazen, yeni bir şey hakkında bilgi edinmenin en iyi yolu diğer her şeyden öğrenmektir.
Bir yanıt yazın